Steady-state Approximations for Hodgkin-Huxley Cell Models: Towards Multi-scale Models of Uterine Smooth Muscle
Abstract¶
The Tong et al. (2011) publication presents a comprehensive mathematical model of electro-mechanical behaviour in a uterine smooth muscle cell. It incorporates ion channel currents into a classic Hodgkin-Huxley membrane voltage formulation as well as Ca2+ concentration dynamics with pumps and exchangers. Mechanical force generation by way of the Hai-Murphy smooth muscle cell model is computed based on the Ca2+ concentrations. The ‘full’ Tong 2011 model (FTM) includes nineteen ordinary differential equations for the ion channel activation/inactivation variables out of a total of 105 equations overall. An effort at reducing the FTM into a smaller number of equations for computational efficiency – the ‘reduced’ Tong model (RTM) – aims at reproducing the overall behaviour of the FTM without excessive detail. We present here the CellML implementation of the RTM for simulating the FTM within the context of the reduced model’s primary publication as derived from the Tong et al. (2011) model.
1Introduction¶
Balancing computational tractability and realism is a persistent concern for mathematical modeling. Of the published uterine smooth muscle cell (USMC) models, the Tong et al. (2011) version is somewhat of a gold standard for the cell type, yet encompasses a substantial computational expense in solving the nineteen ODEs amongst the full suite of 105 equations for the ‘full’ Tong Model (FTM). We present the mathematical model for a ‘reduced’ Tong Model (RTM) aimed at reproducing the overall behaviour of the FTM but with reduced computational expense as developed by Means et al. (2023). Both the FTM and RTM are available in the Physiome Model Repository (PMR) Yu et al., 2011, and we utilise the implementations provided for presenting the results given in the RTM model primary publication of Means et al. (2023) comparing the FTM and RTM simulations.
2Model description¶
2.1Primary Publication¶
The FTM model Tong et al., 2011 assembles numerous ion channel submodels for representing the membrane voltage () with a Hodgkin-Huxley formalism. Of these submodels, the FTM includes one Na+, two Ca2+ (-gated), five K+ as well as a non-specific Cation channel and a ‘hyperpolarisation’ Na+ and K+ channel. These entail a total of nineteen ODEs for activation and inactivation variables. Additional Ca2+ dynamic mechanisms such as a plasma-membrane ATP-ase pump and the Na+-Ca2+ exchanger are included and another exchanger, the Na+-K+ transporter appears as well. [Ca2+]i in turn provides activation of a Hai-Murphy cross-bridge model describing contraction for smooth muscles Hai & Murphy (1988). For the RTM, only the ion channel mechanisms and transporters are considered for reduction; particularly, the activation and inactivation variables are considered in turn for steady-state approximations. The primary paper of Means et al. (2023) is then the focus of the model consideration: comparison between presented results in Means, et al. of the RTM with the FTM is provided in this article demonstrating CellML implementations of both the reduced and full model variants.
2.2CellML Models¶
Implementations of both the FTM and RTM are available in the Physiome Model Repository (PMR) here and here, respectively. This article focuses on the reproduction of results presented in the primary article of Means et al. (2023) and not results presented in Tong et al. (2011), and is thus arranged accordingly.
Individual results of the primary article are then organised according to reproduction of key results from the FTM associated article. Variations of parameters and enabling or disabling of full dynamical variables or utilisation of their steady-state approximating equivalents are noted where suitable.
Two sets of simulations experiments are presented in the results of primary article:
Reproduction of experimental data simulated in Fig. 12 of FTM using the RTM-described ‘Standard Simulation Protocol’:
Applied stimulus, , of -0.5 pA/pF, duration 2 seconds.
, [Ca2+]i and force generation output comparison.
Reproduction of experimental data simulated in Fig. 11 of FTM:
Applied stimulus, , of -0.9 pA/pF, duration 9 seconds.
Applied stimulus, , of -0.4 pA/pF, duration 9 seconds.
Depolarising K+ elevated external concentration.
Applied stimulus, , of -0.3 pA/pF, duration 9 seconds.
Applied stimulus, , of -0.2 pA/pF, duration 49 seconds.
output comparison.
Details of parameter variations are noted in the corresponding figure subtitles as well as referred to in the primary publication.
3Model Results¶
Note, the originating simulation data was generated in OpenCOR, as well as the reproduction for both the FTM and RTM using PMR implementations of the respective CellML models; no extraction of figures was performed for this presentation. All figures generated with CellML implementation with minor variations in applied stimulus strength or duration () conductances (i.e., ) as noted throughout and readily reproducible given said variations when performed manually in the CellML file available at the PMR.
3.1Standard Simulation Protocol (SSP)¶
The SSP formed the basis for a test case of accuracy and performance with the RTM versus the FTM, given above noted parameters of stimulus and duration. All initial conditions of the numerous concentrations, membrane voltage and activation or inactivation variables are as noted in the FTM (and RTM) description. For the FTM, the result is itself a reproduction of experimental traces given in Okabe, et al. Okabe et al., 1999; the result shown in Fig. 1 is generated with the Tong, 2011 PMR CellML implementation. The RTM generates the observed reproduction of results as shown utilising the Reduced Tong, 2011 PMR CellML implementation deploying steady-state approximations of the full model’s ordinary differential equations. Both the FTM and RTM curves are as demonstrated from the originating publication, where the FTM result is shown with black ’+’ and RTM with a blue trace. Differences between them are a result of the reduction method described in the primary publication, Means, et al. Means et al., 2023. Note, all initial conditions and parameter values are set to defaults in the provided CellML implementations at the PMR.
| (a) | 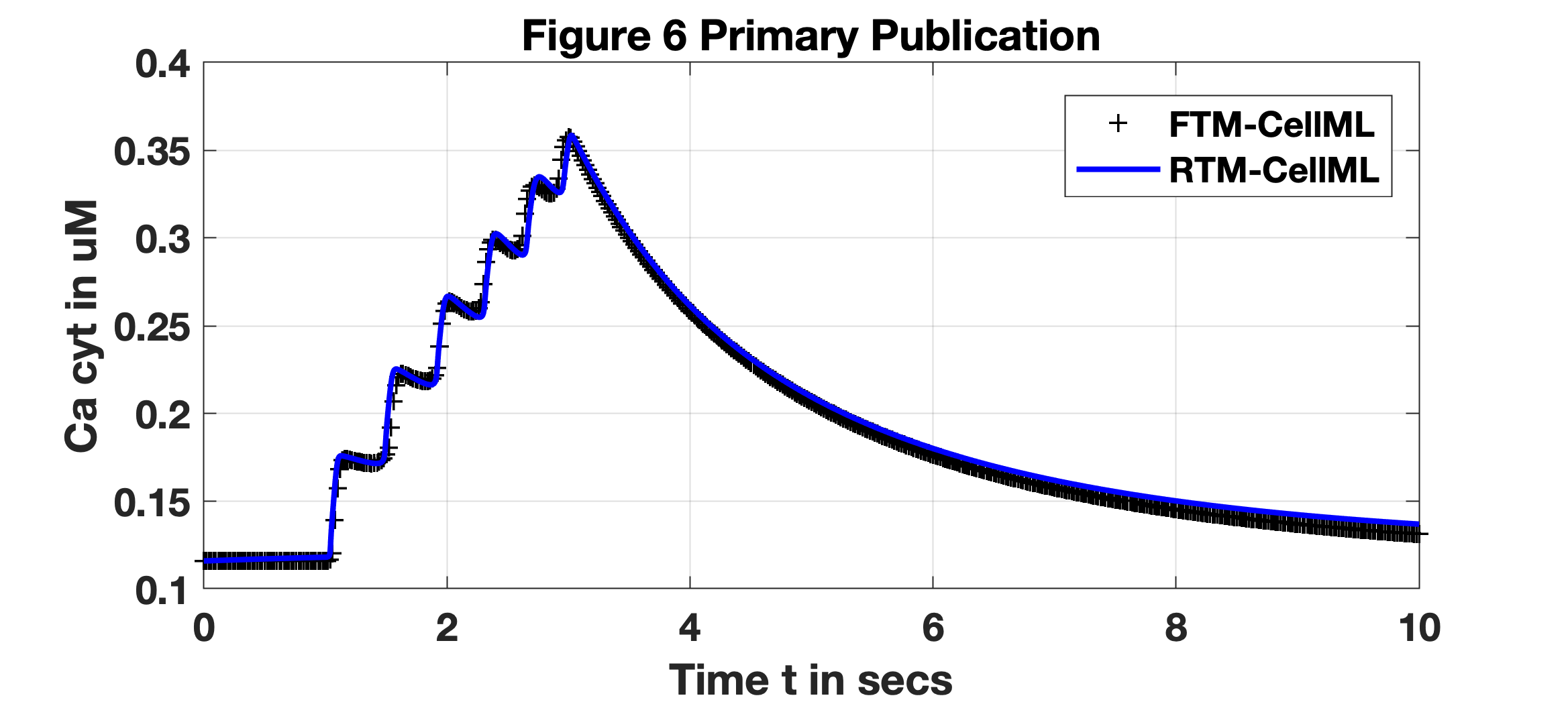 |
|---|---|
| (b) | 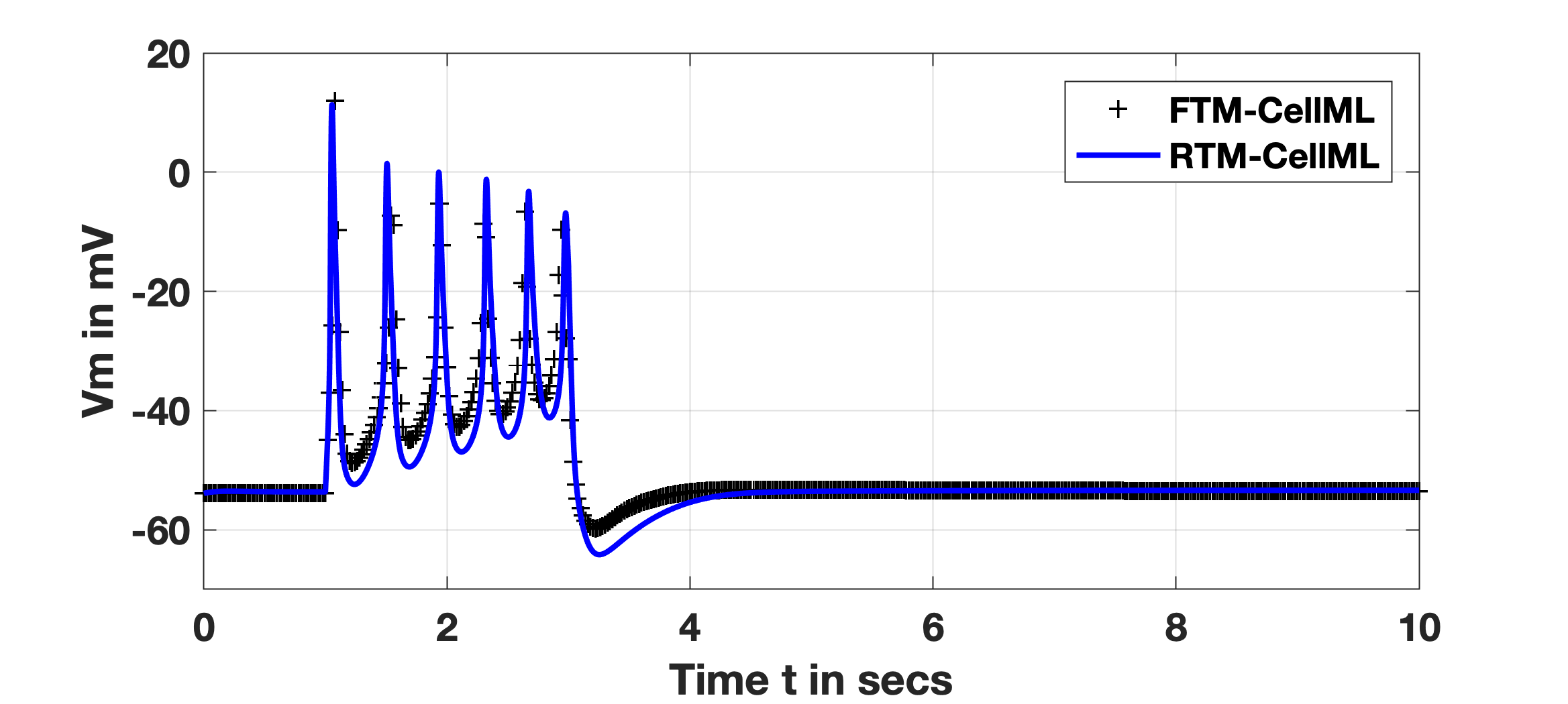 |
| (c) | 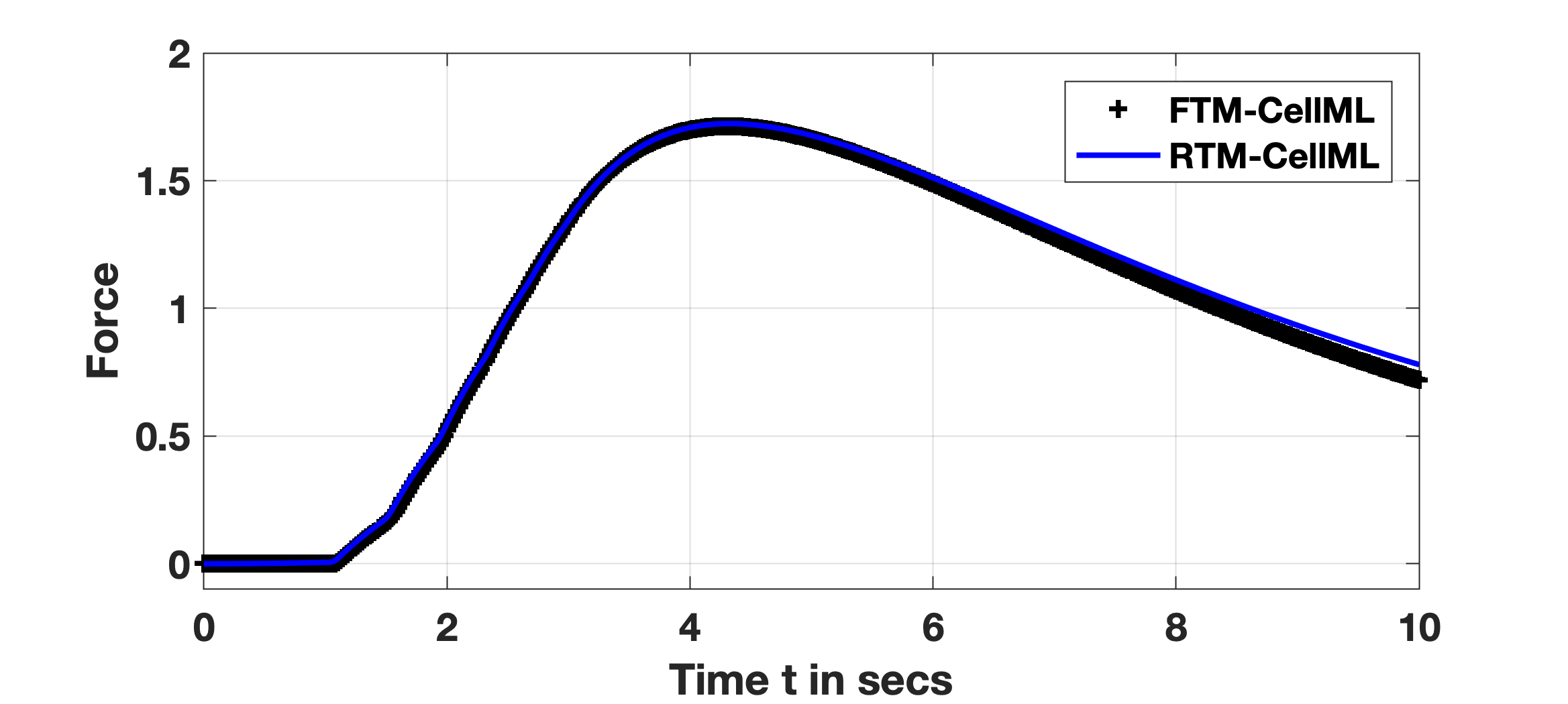 |
Figure 1:SSP Reproduction: FTM and RTM results: black ’+’ and blue trace, respectively. All initial conditions are identical between them with an applied stimulus, of -0.5 pA/pF for two seconds initiated at time secs.
3.2 Variations¶
The primary paper demonstrates functionality of the RTM model as a whole applied to scenarios demonstrated in Figure 11 of the original Tong, et al. paper where applied stimulus, is varied along with a test depolarising pulse of extracellular potassium, . Plots show in this instance data taken from the originating OpenCOR computations for the primary paper (labeled ’Means, et al.’) and regenerating code (’CellML’) with black ’+’ and blue traces, respectively (Figure 2). ’Base case’ for RTM results generated include variations to channel conductances as described in the primary publication; variants thereof described as such as noted primarily include changes to or (see Fig. 2). Deviations in results between the original data traces and reproduction are minimal if at all - particularly with the longer-term stimulus of Panel (e). Each result stems from gradual reduction in with the suite of varied conductances for the channels included in the RTM along with steady-state approximations; note, there is no comparison trace here with the FTM result of Figure 11, Tong, et al. 2011 Tong et al., 2011. Nevertheless, the primary paper results given in Figure 7 of Means, et al. Means et al., 2023 demonstrate production of each trace with the appropriate value of as noted: -0.9, -0.4, -0.3 and -0.2 pA/pF for Panels (a-b) and (d-e). The longer-time duration for these results of 9 seconds and longer with (e) generate the longer set of action potentials as well. Note, Panel (e) includes a variation to the conductance of the potassium channel with = 0.75 pA/pF. Alternatively, Panel (c) of Fig. 2 shows not a variation of but rather effect of a depolarising pulse, where concentration of extracellular K+ is set to 10 mM. These variations are applied manually to the provided RTM CellML implementation available at the PMR; no automated scripts generate these results as of writing this article.
Traces shown in Fig. 2 reproduce results given in Means, et al. aimed at showing ability of RTM to mimic production of the experimental traces of Wilde and Marshall, 1988 Wilde & Marshall, 1988 and Meisheri, 1979 Meisheri et al., 1979, as referenced in Tong, et al. The OpenCOR implementations of both the FTM and RTM variants of Tong, et al. 2011 demonstrate ability to produce results from both Tong, et al., 2011 and Means, et al.
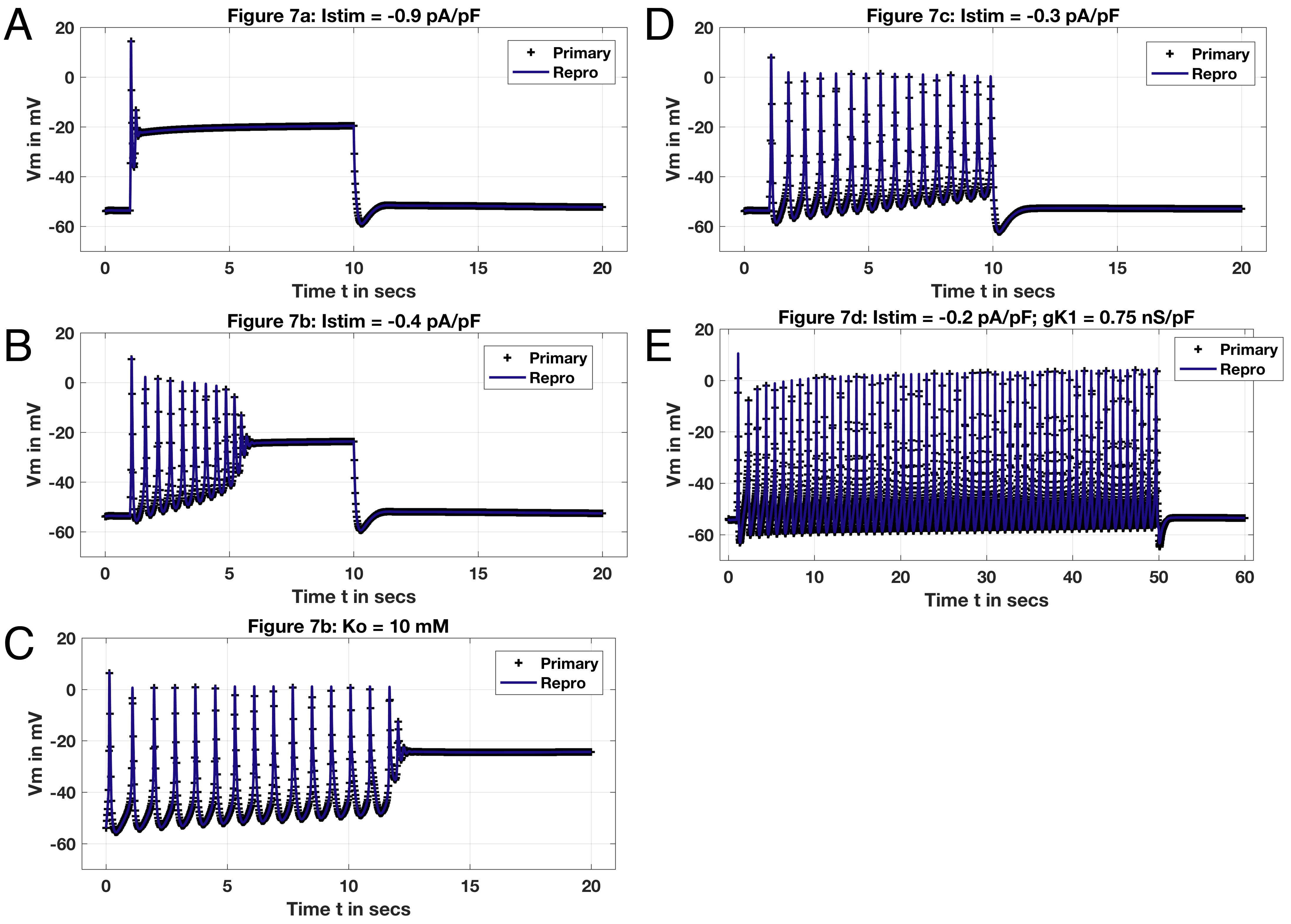
Figure 2:Reproduction of variants. Panel (a): Istim=-0.9 pA/pF, duration 9 seconds ( = 1 to = 10 secs; all parameters identical to base case). Panel (b): Istim=-0.4 pA/pF, duration 9 seconds ( = 1 to = 10 secs; all parameters identical to base case). Panel (c) =0; external pulse 10 mM (all parameters otherwise identical to base case). Panel (d): Istim=-0.3 pA/pF, duration 9 seconds (all parameters identical to base case). Panel (e) Istim=-0.2 pA/pF, duration 49 seconds, =0.75 pA/pF (all parameters otherwise identical to base case).
4Discussion¶
We demonstrated reproducibility of the RTM version of the FTM as shown in the primary article of Means, et al. Means et al., 2023. We utilised the available CellML implementation of the RTM available at the PMR for said demonstration, as well as the FTM implementation for comparisons where noted. Each result shown is a replication of the original results given in Means, et al. with only a minor variation in as noted in for the variants presented in Fig. 2 Panel (e). All results shown here are readily computable by way of the CellML models in the repository with slight modifications to the parameter values and stimulus protocols as detailed above.
Acknowledgments¶
This work was funded, in part, by grants from the New Zealand Ministry of Business Innovation and Employment’s Ministry of Business, Innovation and Employment’s Catalyst: Strategic Fund.
- Tong, W.-C., Choi, C. Y., Kharche, S., Holden, A. V., Zhang, H., & Taggart, M. J. (2011). A computational model of the ionic currents, Ca2+ dynamics and action potentials underlying contraction of isolated uterine smooth muscle. PLoS One, 6(4), e18685. 10.1371/journal.pone.0018685
- Means, S. A., Roesler, M. W., Garrett, A. S., Cheng, L., & Clark, A. R. (2023). Steady-state approximations for Hodgkin-Huxley cell models: Reduction of order for uterine smooth muscle cell model. PLOS Computational Biology, 19(8), 1–23. 10.1371/journal.pcbi.1011359
- Yu, T., Lloyd, C. M., Nickerson, D. P., Cooling, M. T., Miller, A. K., Garny, A., Terkildsen, J. R., Lawson, J., Britten, R. D., Hunter, P. J., & Nielsen, P. M. F. (2011). The Physiome Model Repository 2. Bioinformatics, 27(5), 743–744. 10.1093/bioinformatics/btq723
- Hai, C. M., & Murphy, R. A. (1988). Cross-bridge phosphorylation and regulation of latch state in smooth muscle. Am J Physiol, 254(1 Pt 1), C99-106. 10.1152/ajpcell.1988.254.1.C99
- Okabe, K., Inoue, Y., Kawarabayashi, T., Kajiya, H., Okamoto, F., & Soeda, H. (1999). Physiological significance of hyperpolarization-activated inward currents (Ih) in smooth muscle cells from the circular layers of pregnant rat myometrium. Pflugers Arch, 439(1–2), 76–85. 10.1007/s004249900140
- Wilde, D. W., & Marshall, J. M. (1988). Effects of tetraethylammonium and 4-aminopyridine on the plateau potential of circular myometrium from the pregnant rat. Biol Reprod, 38(4), 836–845. 10.1095/biolreprod38.4.836
- Meisheri, K. D., McNeill, J. H., & Marshall, J. M. (1979). Effect of isoproterenol on the isolated pregnant rat myometrium. Eur J Pharmacol, 60(1), 1–6. 10.1016/0014-2999(79)90045-1





