Incorporation of sarcolemmal calcium transporters into the Shorten et al. (2007) model of skeletal muscle: equations, coding and stability
Abstract¶
We describe a major development of the Shorten et al. (2007) model of skeletal muscle electrophysiology, biochemistry and mechanics. The model was developed by incorporating equations for sarcolemmal transport of calcium ions, including L-type calcium channel, sodium-calcium exchange, calcium pump and background calcium channel. The extended model also includes an addition to the equations for extracellular potassium ion movements to enable the exchange of potassium ions between bulk (plasma) concentration and the interstitial and tubular compartments to be modelled. In further research in an accompanying paper (Tasaki et al, 2019), we succeeded in reproducing muscle cramp, as well as its prevention and reversal, by investigating muscle contraction and cramp using this extended model in comparison with the original model.
1Introduction¶
The aim of this paper is to extend the Shorten et al. (2007) skeletal muscle model to include surface membrane calcium transporters. This is necessary to enable the model to be used in applications involving interactions between the surface transporters and either drugs or ions. The extended model was developed specially for a project involving a medication that acts on L-type calcium channels described in an accompanying article (Tasaki et al. 2019).
2Model description¶
2.1Original model¶
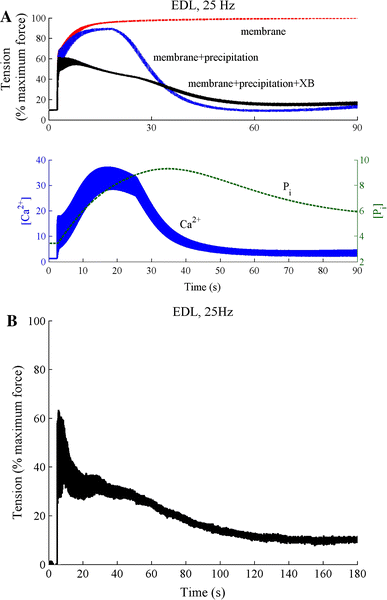
Figure 1:A - Simulation of force development in the extensor digitorum longus (EDL) fast-twitch version of the model to 90 seconds stimulation at 25 Hz. The curves show the total fatigue response (membrane+precipitation+cross-bridge) along with the responses with no myoplasmic phosphate (Pi) build-up (membrane) and no Pi feedback on the cross-bridge dynamics (membrane+precipitation). Also shown are the calcium and Pi dynamics in a fibre exhibiting total fatigue response (membrane+precipitation+cross-bridge). Once the Pi exceeds a critical threshold it precipitates with SR calcium to reduce calcium release from the SR and cross-bridge cycling kinetics. B - the measured EDL response to sustained 25 Hz stimulation. (reprinted with permission from Shorten et al. (2007))
The skeletal muscle model developed by Shorten et al. (2007) is extensive. It includes models of the action potential, electromechanical coupling, the cross-bridge reactions, and the immediate biochemical processes of consumption of ATP and concentrations of inorganic phosphate. The model was also parameterised to fast and slow twitch fibre types, which have a number of biochemical and biophysical differences. These differences are related to the different force/fatigue responses in fast and slow twitch fibres that are not well understood. A better understanding of the cascade of biochemical and physical events underlying skeletal muscle fatigue will provide a basis for targeted intervention by nutritional or other means to improve muscle function. Loss of muscle function is a major issue in elite athletes, cachectic subjects and those undergoing aging, where muscle function decreases after the age of 40.
The model is available in full working order from the Physiome Model Repository (PMR) at https://
Since the model includes the immediate biochemical energetic processes, including variations in ATP and phosphate, it can reproduce the sequence of events underlying muscle fatigue, as shown in Figure 1. Phosphate is generated during cross-bridge cycling.
2.2Explanation why sarcolemmal calcium transporters need to be incorporated¶
Electromechanical coupling in smooth and cardiac muscle depends on calcium influx. In both types of muscle, release of calcium ions from the sarcoplasmic reticulum is triggered by calcium-induced calcium release. By this process, a small calcium influx is amplified to produce sufficient calcium to initiate cross-bridge reactions and so produce sliding filament contraction. By contrast, electromechanical coupling in skeletal muscle is purely electrical. Tight coupling between T-tubule membranes through which the action potential propagates makes it possible for SR calcium release to occur even if no calcium influx occurs through the sarcolemmal membrane. Skeletal muscle contractions can therefore continue to occur even in the absence of extracellular calcium. This was demonstrated by Edman & Grieve (1964). The immediate effect of exposure of a frog skeletal muscle to nearly zero external calcium was that the muscle continued to contract. Cairns et al. (1998) found a similar result in mammalian skeletal muscle. Nominally, calcium-free solutions “had little effect on tetanic force in non-fatigued muscle.”
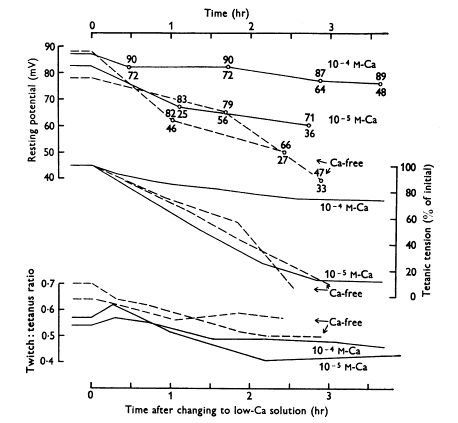
Figure 2:Effect of lowering calcium concentration in the solution bathing a frog sartorius muscle on mean resting potentials (upper curves; total range of potentials also shown), tetanic tensions (middle curves) and the twitch:tetanus ratio (lower curves). Frog sartorius muscle, temperature 0-1 C. Square pulses of 1 ms duration were applied through two wire electrodes so as to stimulate the whole muscle. Calcium-free solution contained 0.1 mM EDTA. (Reprinted with permission from Edman & Grieve (1964)).
However, during prolonged exposure to very low calcium, the twitch contractions fall. In Figure 2, the muscles were exposed to either 0.1 mM, 0.01 mM calcium or calcium-free Ringer’s solution. Both tetanic tension and the twitch:tetanus ratio slowly declined. This result implies that over long periods of time skeletal muscle does depend on sarcolemmal calcium influx. See Cairns Cairns et al., 2003Cairns & Lindinger, 2008 for more discussion on the role of extracellular calcium.
It is therefore important to incorporate surface membrane calcium fluxes in the Shorten et al. (2007) model.
2.3Methods of incorporating sarcolemmal calcium transporters¶
L-type calcium current
The CaV 1.1 and CaV 1.2 L-type calcium channels are found in adult skeletal muscle Jeftinija et al., 2007Flucher & Tuluc, 2017 . CaV 1.1 is restricted to the T-tubules and CaV 1.2 is expressed in the sarcolemma of type I and IIa myofibers, but not IIb fibres. The data and equations for the L-type calcium current (ICaL) were obtained from the work of Wang et al. (2008) who studied the effect of a sodium channel blocker, Riluzole, on the action potential in cultured human skeletal muscle cells. The equations were taken from the Physiome Model Repository:
https://
The equations are:
The equation for the inactivation (f) process was added for use in a future project.
Sodium-calcium exchange
The data and equations for sodium-calcium exchange (NCX) were obtained from Noble et al. (1991), which were originally developed by Di Francesco & Noble (1985) and which reproduce the data obtained by Kimura et al. (1987) for cardiac muscle. NCX is based on 3:1 stoichiometry Michel et al., 2014. NCX is also more abundant in slow twitch fibres, which is consistent with a role for NCX in fatigue resistance Michel et al., 2014.
The equation is:
Calcium pump
The data and equations for the calcium pump current, IpCa, were obtained from Lindblad et al. (1996) in cardiac muscle.
The equation is:
Background calcium leak
The data and equations for the background calcium current leak, IbCa, were obtained from Noble et al. (1991).
The equation is:
g was usually set to zero. The calcium pump and sodium-calcium exchange were sufficient to balance calcium movements in steady state conditions.
To represent the bulk potassium concentration outside the muscle, [K]b (which is equivalent to a plasma potassium concentration), we added a term to the differential equation for interstitial potassium, K, which then becomes:
[K] is assumed to be fixed.
The original CellML file along with all the codes can be found in the following link in the PMR:
https://
It is worth to mention that in order to be able to run python scripts the corresponding sedml and cellml files need to be downloaded in the same folder. Also In order to be able to run sedml file the corresponding cellml file needs to be downloaded in the same folder.
3Model results¶
All simulations were run using OpenCOR (version 0.6) Garny & Hunter, 2015
Comparison with the original model over short pulse trains
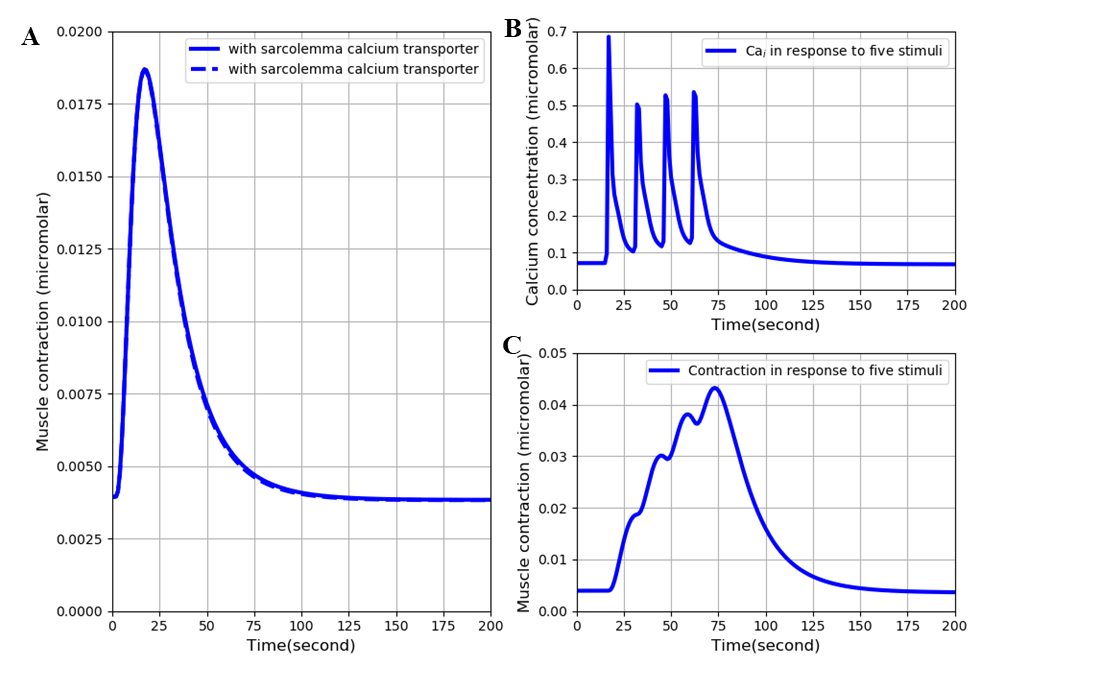
Figure 3:A: superimposed contraction responses to a single stimulus with and without (lighter curve) the surface calcium transporters. B: free intracellular calcium and C: contraction in response to a train of five stimuli at 15-second intervals. The results are similar to those of Figures 6 and 11 in the original Shorten et al. (2007) model. The results presented in the left panel can be reproduced with the Fig03(L).py script in OpenCOR and those in the right panel with Fig03(R).py
Figure 3 shows the results of calculating the free intracellular calcium and contraction following a single pulse and a short train of 5 stimuli with and without the surface calcium transporters. The simulation files Fig03(L).sedml and Fig03(R).sedml contain the computational setting for running the model with a single pulse and 5 stimuli respectively.
The difference between the results with and without the surface calcium transporters is very small. Adding those transporters does not therefore significantly affect the behaviour of the model over short time periods. This result would be expected since the surface calcium fluxes are very small and do not have much impact on intracellular ion concentrations when short durations are considered.
The curves also compare well qualitatively with Figures 6 and 11 in the original model paper. There is, however, an important quantitative difference arising from the fact that we used initial conditions obtained from running the extended model for very long periods (hours) to achieve steady state conditions. With the original model parameters, this produces a lower initial state of intracellular calcium and, therefore, much lower contraction than in the Shorten et al. (2007). paper.
We also ran these computations using the initial conditions, i.e. not steady state conditions, obtained from the CellML file for the original model on PMR. These results were very similar qualitatively to those shown in Figure 3, except that the contraction was much larger. There was nevertheless still a difference from the published Shorten et al. (2007) paper. The contraction was found to be about 50% of that in the original paper.
Test of calcium balance
Although the equations for influx of calcium through ICaL were obtained on skeletal muscle, the equations for efflux of calcium via sodium-calcium exchange and the calcium pump were obtained from heart muscle models. NCX1 is expressed in high levels in cardiac muscle. NCX1 is also found in skeletal muscle Cifuentes et al., 2000, where it is found in sarcolemma and T-tubule membranes Sacchetto et al., 1996. The major function of the skeletal muscle NCX appears to be to transport calcium out of the cell after contraction.
Their role in the model is to balance the influx and efflux so that over many cycles of normal physiological muscle activity there would be no net change in calcium content of the muscle fibres. We adjusted their amplitudes until balance was achieved, as shown in Figure 4. The simulation file Fig04.sedml contains the computational setting for running the model.

Figure 4:Extended EDL model. Traces are: A - membrane potential, B - calcium current, C - SR calcium, D - free intracellular calcium, E - twitch contraction. The frequency of stimulation is 1 Hz. All parameters are in steady state conditions over 30 cycles of stimulation. The results presented in this figure can be reproduced with the Fig04.sedml
Effect of blocking calcium influx
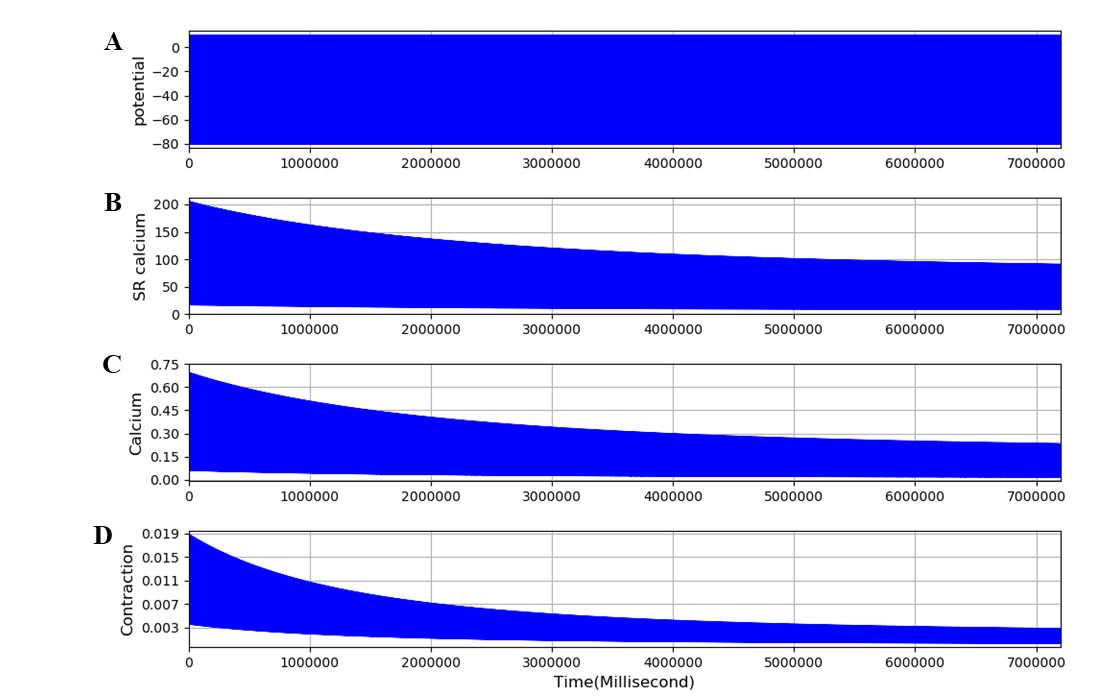
Figure 5:Extended model run for 2 hours with the L-type calcium channel completely blocked. Traces are: A - membrane potential, B - calcium current, C - SR calcium, D - free intracellular calcium, E - twitch contraction. The frequency of stimulation is 0.1 Hz. The results presented in this figure can be reproduced with the Fig05.sedml
Figure 5 shows that, when the L-type calcium channel is blocked, the model is no longer in a steady state. SR calcium, free intracellular calcium and contraction all decline slowly, as observed by Edman & Grieve (1964) in their experiments in skeletal muscle in low or zero external calcium. The model achieves a new steady state after 1-2 hours. This very slow change and its experimental validation is dealt with in a further paper (Tasaki et al., 2019). The simulation file Fig05.sedml contains the computational setting for running the model. In addition to incorporating equations for surface membrane calcium fluxes, we added a term to the extracellular potassium equations to represent the movement of potassium ions between extracellular spaces (interstitial and tubular) within the muscle structure and the spaces outside the muscle, which would include blood plasma potassium. This feature of the extended model is used in an accompanying paper (Tasaki et al., 2019) to model the effects of potassium wash-out during increased blood flow. Figure 6 shows that the equations behave as expected. The bulk (plasma) potassium, [K]b, was switched suddenly between 5 and 2 mM twice during the calculation. The time constant, TauK3, was arbitrarily set to 4 seconds to represent fast perfusion of the interstitial space. Interstitial potassium correctly follows an exponential decline when [K]b is switched to 2 mM and recovers equally rapidly when [K]b is returned to 5mM. The use of this process in representing perfusion of the interstitial space is shown in the accompanying paper (Tasaki et al., 2019). The simulation file Fig06.sedml contains the computational setting for running the model.
![Extended model run for 10 minutes. [K]b was initially set at 5 mM and then switched to 2 mM and later returned to 5 mM. A - Interstitial potassium correctly responds to these changes. B - The membrane potential also responds correctly. The results presented in can be reproduced with the Fig06.py script in OpenCOR](https://pub.curvenote.com/036a7da8-7609-4b8d-870e-743f0ba9b4be/public/fig06-ea541341b03f7823b2b938b3a8900f44.png)
Figure 6:Extended model run for 10 minutes. [K]b was initially set at 5 mM and then switched to 2 mM and later returned to 5 mM. A - Interstitial potassium correctly responds to these changes. B - The membrane potential also responds correctly. The results presented in Figure 6 can be reproduced with the Fig06.py script in OpenCOR
Deficiency of the extended model
As already noted, when the results shown in Figures 4 and 5 are examined carefully, the magnitude of the contractions is clearly very much smaller than in the original Shorten et al. (2007) model. The computed steady state cross-bridge reactions are much less than 1 µM, whereas in the original model the reactions are at least an order of magnitude larger. The reason for this discrepancy is that the model was not parameterised for very long runs, of hours rather than minutes. All our computations are performed when the extended model has achieved steady state after about 2 hours since we need a steady state condition to study the dynamics of change from the steady state when the model is perturbed, e.g. by partial or complete block of the L-type calcium channel, as done in the accompanying paper (Tasaki et al., 2019).
We therefore investigated whether a simple parameter change could restore the magnitude of steady state contraction after very long time periods. Since the low value of calcium and contraction after 2 hours represents a loss of sarcoplasmic reticulum calcium, we investigated the effect of increasing the uptake rate for calcium entry into the SR, nuSR. Figure 7 shows that this simple parameter change can indeed increase the steady state contraction by more than an order of magnitude. When nuSR is increased to 35 the contraction increases from around 0.02 to 0.8. The simulation file Fig07.sedml contains the computational setting for running the model for only one value of nuSR. Peak value of contraction was plotted versus different nuSR (5, 15, 25, 35).
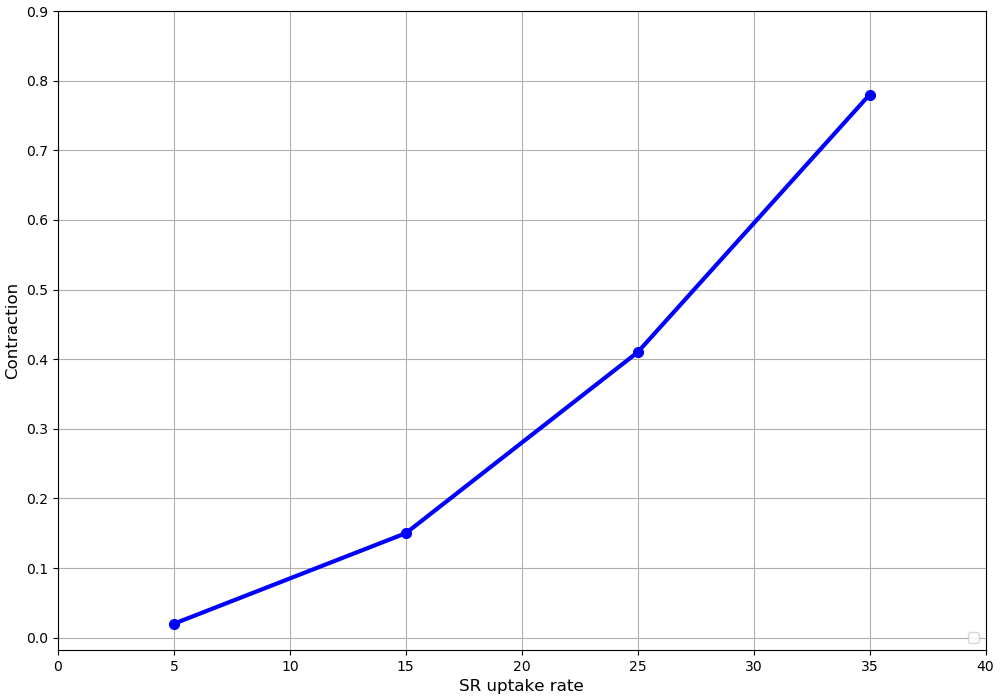
Figure 7:Computed relation between the SR uptake rate, nuSR, and the steady state contraction at a frequency of stimulation of 0.1 Hz. The standard value of nuSR, 4.875, allows the SR to empty over long periods so that the cross-bridge activation by released calcium is very small. Increasing nuSR to 15, 35 and 45 5produces much larger contractions. The results presented in Figure 7 can be reproduced with the Fig07.py and Fig07-plot.py script in OpenCOR
However, the results also showed that further increase of nuSR (e.g to 45) prevented the membrane potential from fully repolarizing. The reason is that the increased calcium release during each contraction activates the sodium-calcium exchange, so producing a larger after-potential.
There is therefore a deficiency that requires further re-parameterisation of the extended model in future applications.
4Discussion¶
Sarcolemmal calcium influx is not necessary for individual twitch responses in skeletal muscle since the membrane trigger for electromechanical coupling is entirely electrical, independent of calcium current. This property is what enabled Shorten et al. (2007) to reproduce fatigue in their model with only intracellular recycling of calcium.
However, by adding equations for the sarcolemmal calcium fluxes we have shown that over periods of time greater than a few seconds, the sarcolemmal calcium fluxes would be expected to have a significant effect. Specifically, the small fluxes gradually alter SR calcium and intracellular free calcium. These changes in calcium concentrations then produce changes in contraction. The slow time course of those changes corresponds to the dynamics of change in contraction observed experimentally when calcium influx is reduced, as shown in the accompanying paper (Tasaki et al., 2019). The influences of changes in sodium, potassium and calcium ion concentrations, on the contraction of skeletal muscle are very complex Cairns et al., 1998Cairns et al., 2003Cairns & Lindinger, 2008. Future work on the extended model needs to be done to determine the extent to which the model could help to clarify these effects.
Further work also needs to be done to explore parameter sets that would increase the steady state contraction to be comparable to the contraction level calculated in the original model. A possible way forward to be developed in the future would be to rebalance the proportion of calcium efflux attributable to sodium-calcium exchange compared to the sarcolemmal calcium pump. The sodium-calcium exchange produces a depolarizing current, whereas the calcium pump does not do so. We have not systematically explored this question in this paper since it is likely that other parameter adjustments may also be required. The parameter space to be explored may be quite large.
Acknowledgments¶
We express our gratitude to TSUMURA & CO. for funding the “University of Oxford Innovative Systems Biology Project sponsored by Tsumura”.
- Shorten, P. R., O’Callaghan, P., Davidson, J. B., & Soboleva, T. K. (2007). A mathematical model of fatigue in skeletal muscle force contraction. Journal of Muscle Research and Cell Motility, 28(6), 293–313. http://dx.doi.org/10.1007/s10974-007-9125-6
- Edman, K., & Grieve, D. (1964). On the role of calcium in the excitation-contraction process of frog sartorius muscle. The Journal of Physiology, 170(1), 138.
- Cairns, S. P., Hing, W. A., Slack, J. R., Mills, R. G., & Loiselle, D. S. (1998). Role of extracellular [Ca2+] in fatigue of isolated mammalian skeletal muscle. Journal of Applied Physiology, 84(4), 1395–1406.
- Cairns, S. P., Buller, S. J., Loiselle, D. S., & Renaud, J.-M. (2003). Changes of action potentials and force at lowered [Na+] o in mouse skeletal muscle: implications for fatigue. American Journal of Physiology-Cell Physiology, 285(5), C1131–C1141.
- Cairns, S., & Lindinger, M. (2008). Do multiple ionic interactions contribute to skeletal muscle fatigue? The Journal of Physiology, 586(17), 4039–4054.
- Jeftinija, D. M., Wang, Q. B., Hebert, S. L., Norris, C. M., Yan, Z., Rich, M. M., & Kraner, S. D. (2007). The CaV 1.2 Ca2+ channel is expressed in sarcolemma of type I and IIa myofibers of adult skeletal muscle. Muscle & Nerve: Official Journal of the American Association of Electrodiagnostic Medicine, 36(4), 482–490.
- Flucher, B. E., & Tuluc, P. (2017). How and why are calcium currents curtailed in the skeletal muscle voltage-gated calcium channels? The Journal of Physiology, 595(5), 1451–1463.
- Wang, Y.-J., Lin, M.-W., Lin, A.-A., & Wu, S.-N. (2008). Riluzole-induced block of voltage-gated Na+ current and activation of BKCa channels in cultured differentiated human skeletal muscle cells. Life Sciences, 82(1–2), 11–20.
- Noble, D., Noble, S., Bett, G., Earm, Y., Ho, W., & So, I. (1991). The Role of Sodium-Calcium Exchange during the Cardiac Action Potential a. Annals of the New York Academy of Sciences, 639(1), 334–353.
- Di Francesco, D., & Noble, D. (1985). A model of cardiac electrical activity incorporating ionic pumps and concentration changes. Philosophical Transactions of the Royal Society of London. B, Biological Sciences, 307(1133), 353–398.
- Kimura, J., Miyamae, S., & Noma, A. (1987). Identification of sodium-calcium exchange current in single ventricular cells of guinea-pig. The Journal of Physiology, 384(1), 199–222.
- Michel, L. Y., Verkaart, S., Koopman, W. J., Willems, P. H., Hoenderop, J. G., & Bindels, R. J. (2014). Function and regulation of the Na+-Ca2+ exchanger NCX3 splice variants in brain and skeletal muscle. Journal of Biological Chemistry, 289(16), 11293–11303.
- Lindblad, D., Murphey, C., Clark, J., & Giles, W. (1996). A model of the action potential and underlying membrane currents in a rabbit atrial cell. American Journal of Physiology-Heart and Circulatory Physiology, 271(4), H1666–H1696.
- Garny, A., & Hunter, P. J. (2015). OpenCOR: a modular and interoperable approach to computational biology. Frontiers in Physiology, 6, 26.
- Cifuentes, F., Vergara, J., & Hidalgo, C. (2000). Sodium/calcium exchange in amphibian skeletal muscle fibers and isolated transverse tubules. American Journal of Physiology-Cell Physiology, 279(1), C89–C97.





