The cardiac Na⁺/K⁺ ATPase: An updated, thermodynamically consistent model
Abstract¶
The Na/K ATPase is an essential component of cardiac electrophysiology, maintaining physiological Na and K concentrations over successive heart beats. Terkildsen et al. (2007) developed a model of the ventricular myocyte Na/K ATPase to study extracellular potassium accumulation during ischaemia, demonstrating the ability to recapitulate a wide range of experimental data, but unfortunately there was no archived code associated with the original manuscript. Here we detail an updated version of the model and provide CellML and MATLAB code to ensure reproducibility and reusability. We note some errors within the original formulation which have been corrected to ensure that the model is thermodynamically consistent, and although this required some reparameterisation, the resulting model still provides a good fit to experimental measurements that demonstrate the dependence of Na/K ATPase pumping rate upon membrane voltage and metabolite concentrations. To demonstrate thermodynamic consistency we also developed a bond graph version of the model. We hope that these models will be useful for community efforts to assemble a whole-cell cardiomyocyte model which facilitates the investigation of cellular energetics.
1Introduction¶
Cardiomyocytes maintain Na and K ions within their physiological concentration range, in part by using Na/K ATPases located on their plasma membranes. The Na/K ATPase is an electrogenic ion pump that uses energy from ATP hydrolysis to drive the transport of Na and K ions against an electrochemical gradient. A previous model of the cardiomyocyte Na/K ATPase was developed by Terkildsen et al. (2007) and subsequently incorporated into a whole-cell cardiomyocyte model to demonstrate that reduced Na/K ATPase activity plays a dominant role in extracellular potassium accumulation during ischaemia Terkildsen et al., 2007Terkildsen, 2006. In this manuscript the Na/K ATPase model of Terkildsen et al. (2007) will subsequently be referred to as the Terkildsen et al. model.
The Na/K ATPase model presented in Terkildsen et al. (2007) was based upon an earlier implementation which proposed thermodynamic constraints and a lumping scheme for model simplification Smith & Crampin, 2004. A key development was that the Terkildsen et al. model could reproduce a wider range of data which captured the dependence of the pump current upon membrane voltage Nakao & Gadsby, 1989, extracellular sodium Nakao & Gadsby, 1989, intracellular sodium Hansen et al., 2002, extracellular potassium Nakao & Gadsby, 1989 and MgATP Friedrich et al., 1996. Unfortunately the cycling velocity figures presented within the original paper are not reproducible using information supplied in the figure legends Terkildsen et al., 2007, Fig. 2 and code used to generate those figures was not publicly archived. These issues are exacerbated by apparent errors within the reported equations and parameter values (further described in Section 2) which result in physical and thermodynamic inconsistencies.
Here we address these issues, updating the model to ensure that it is thermodynamically consistent, and archiving MATLAB and CellML Lloyd et al., 2004 code for reproducibility. This required the modification of several equations (Section 2) and re-parameterisation through fitting to the original data (Section 3). To verify the physical plausibility of the updated model we have also developed a bond graph version Oster et al., 1971Gawthrop & Crampin, 2014, and we refer readers to Gawthrop & Smith (1996); Borutzky (2010); and Gawthrop & Bevan (2007) for further information on bond graph theory. Given the thermodynamic consistency of our updated model we believe that it is particularly well-suited for incorporation into community efforts for developing a thermodynamic model of a cardiomyocyte to ultimately study whole-heart cardiac energetics.
2Modifications¶
The Terkildsen et al. model uses the Post-Albers cycle Apell, 1989, a model in which sodium and potassium ions bind individually on one side of the membrane, and unbind on the other side (Figure 1). The full Post-Albers cycle was simplified to reduce computational complexity by assuming that faster reactions are in rapid equilibrium, reducing the full 15-state model to a four-state model with eight modified rate constants Smith & Crampin, 2004. The entire cycle was then assumed to be in steady-state such that the model simplified to a single equation for cycling velocity, with metabolite dependence incorporated in a manner that accounted for thermodynamic constraints. We identified three issues while reimplementing the Terkildsen et al. model, and made several modifications to remedy these issues:
Issue 1: Equilibrium constants were inconsistent with the number of binding sites. For identical binding sites the kinetic rate constants are typically assumed to be proportional to the number of sites available for binding/unbinding Keener & Sneyd, 2009 and we modified the reaction scheme from Terkildsen et al. (2007) to achieve this (red parameters within Figure 1).
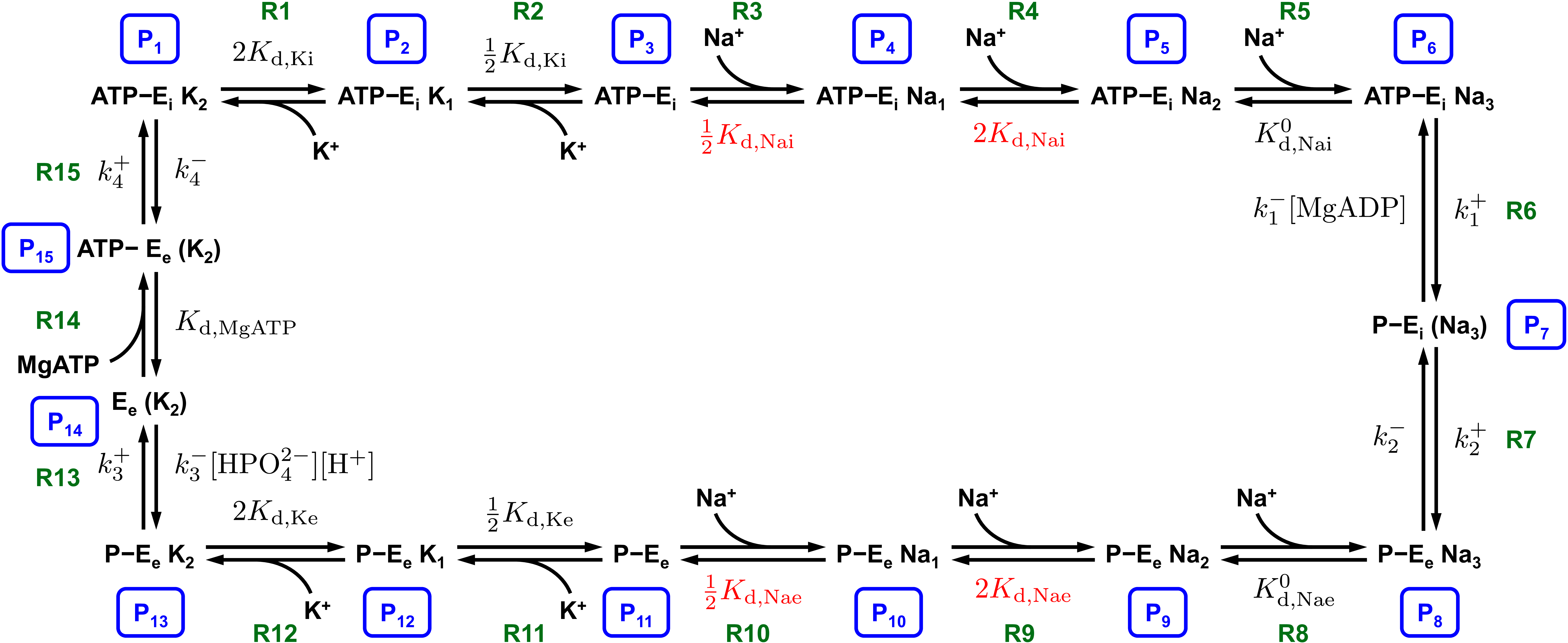
Figure 1:Reaction scheme of the cardiac Na/K ATPase model. Numbers for each pump state (blue boxes) and reaction names (green) are labelled, with corrected parameters shown in red.
Issue 2: The detailed balance constraint used during fitting procedure appears to have used an incorrect parameter value with important consequences on the thermodynamic consistency of the model. This constraint relates the kinetic constants defined in Figure 1:
where J/mol/K is the universal gas constant, is the absolute temperature, and is the standard free energy of MgATP hydrolysis at pH 0. It appears that Terkildsen et al. (2007) started with a standard free energy of at pH 7, but adjusted to a physiological pH rather than pH 0. As a result, substituting the model parameter values into equation (1) results in , which is inconsistent with the typical standard free energy of at 311K Tran et al., 2009Guynn & Veech, 1973. At a temperature of 310K this results in an overall equilibrium constant over -fold greater than the correct value. Thus we use within the detailed balance constraint.
Issue 3: The lumping scheme used to reduce the 15-state model to a 4-state model with modified kinetic constants was similar to Smith & Crampin (2004), however with the updated assignment of electrical dependence in Terkildsen et al. (2007) some expressions were not applicable. As a result, expressions for several modified rate constants (, , and ) were incorrect, leading to inaccurate representations of pump kinetics. We have corrected the equations for these modified rate constants:
where
and is the unit of charge translocated by the final sodium binding reaction R5. We derive an expression for , and expressions for the other modified rate constants follow similarly. Since the pump states 1 to 6 are lumped together, the constant is scaled according to the ratio between the amount of state 6 and the total amount of states 1–6. If we represent as the molar amount of state , then:
Because it was not possible to fix the above issues without significantly changing the kinetics of the model, we subsequently had to reparameterise the Terkildsen et al. model such that it would be physically and thermodynamically consistent. In subsequent sections, we shall refer to the reparameterised model with updated equations as the “updated model” and the model with equations and parameters described in Terkildsen et al. (2007) as the “original model”.
3Reparameterisation of the model¶
Using the updated model’s equations, we fitted parameters to data from Terkildsen et al. (2007)Terkildsen (2006). After setting to in the thermodynamic constraint, Equation (1), we parameterised the updated model using similar methods to the original model Terkildsen, 2006 which minimised an objective function describing divergence of the model from experimental data. Minor changes to the fitting procedure include:
The weighting for extracellular potassium above 5.4 mM for the data of Nakao & Gadsby (1989) was increased from to to obtain a reasonable fit at physiological concentrations.
To ensure that cycling velocity magnitudes matched Nakao & Gadsby (1989), the curve for was fitted without normalisation.
Rather than using a local optimiser with literature sources for initial parameter estimates, we minimised the objective function by using particle swarm optimisation Kennedy & Eberhart, 1995 followed by a local optimiser to find a global minimum.
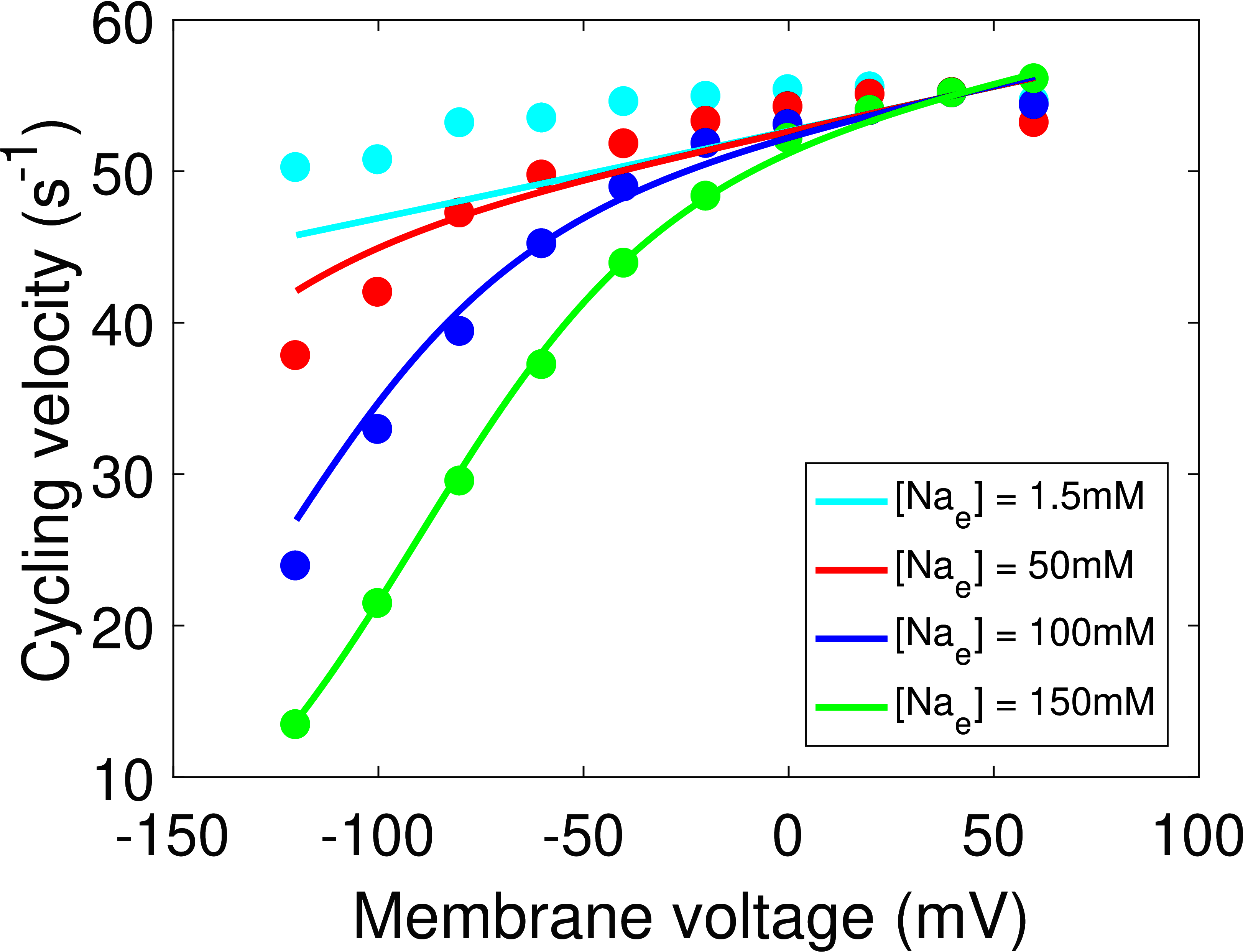
The updated model provides good fits to each data source (Figures 2 & 3), and the quality of fits are comparable to Terkildsen (2006), although we achieved a slightly worse fit at lower extracellular sodium concentrations (Figure 2(A)). It should be noted, however, that our model appears to be more consistent with experimental data that suggest saturated cycling velocity at positive membrane potentials is relatively insensitive to extracellular sodium (Figure 2(B)) Nakao & Gadsby, 1989. Updated model parameters are given in Table 1 of Section 8.
| A | |
|---|---|
 | |
| B | |
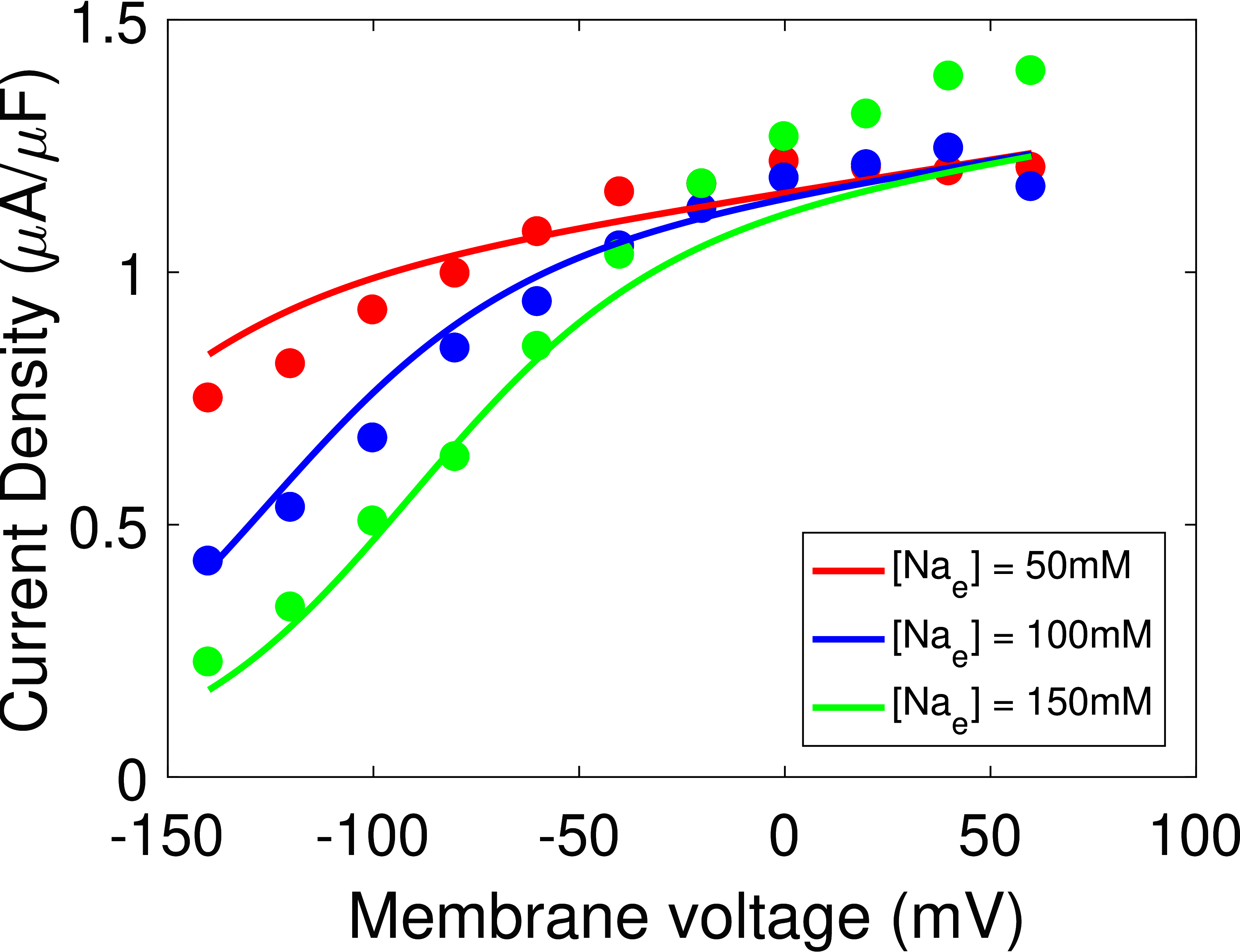 |
Figure 2:Model fit of the updated cardiac Na/K ATPase model to current-voltage measurements. (A) Comparison of the model to extracellular sodium and voltage data Nakao & Gadsby, 1989, Fig. 3, with cycling velocities scaled to a value of at . (B) Comparison of the model to whole-cell current measurements Nakao & Gadsby, 1989, Fig. 2(a).
| A | |
|---|---|
![Model fit of the updated cardiac Na^+/K^+ ATPase model to metabolite dependence data. Simulation conditions are displayed on the right of each figure. (A) Comparison of the model to data with varying intracellular sodium concentrations , normalised to the cycling velocity at \mathrm{[Na]_i = 50\si{mM}}. (B) Comparison of the model to data with varying extracellular potassium , normalised to the cycling velocity at \mathrm{[K]_e = 5.4\si{mM}}. (C) Comparison of the model to data with varying ATP , normalised to the cycling velocity at \mathrm{[MgATP] = 0.6\si{mM}}.](https://pub.curvenote.com/df91f02c-1660-414b-b636-0f83e7abfb19/public/Terkildsen_fit_Hanse-1809f9801798210a34b67685e56d23b6.png) | |
| B | |
 | |
| C | |
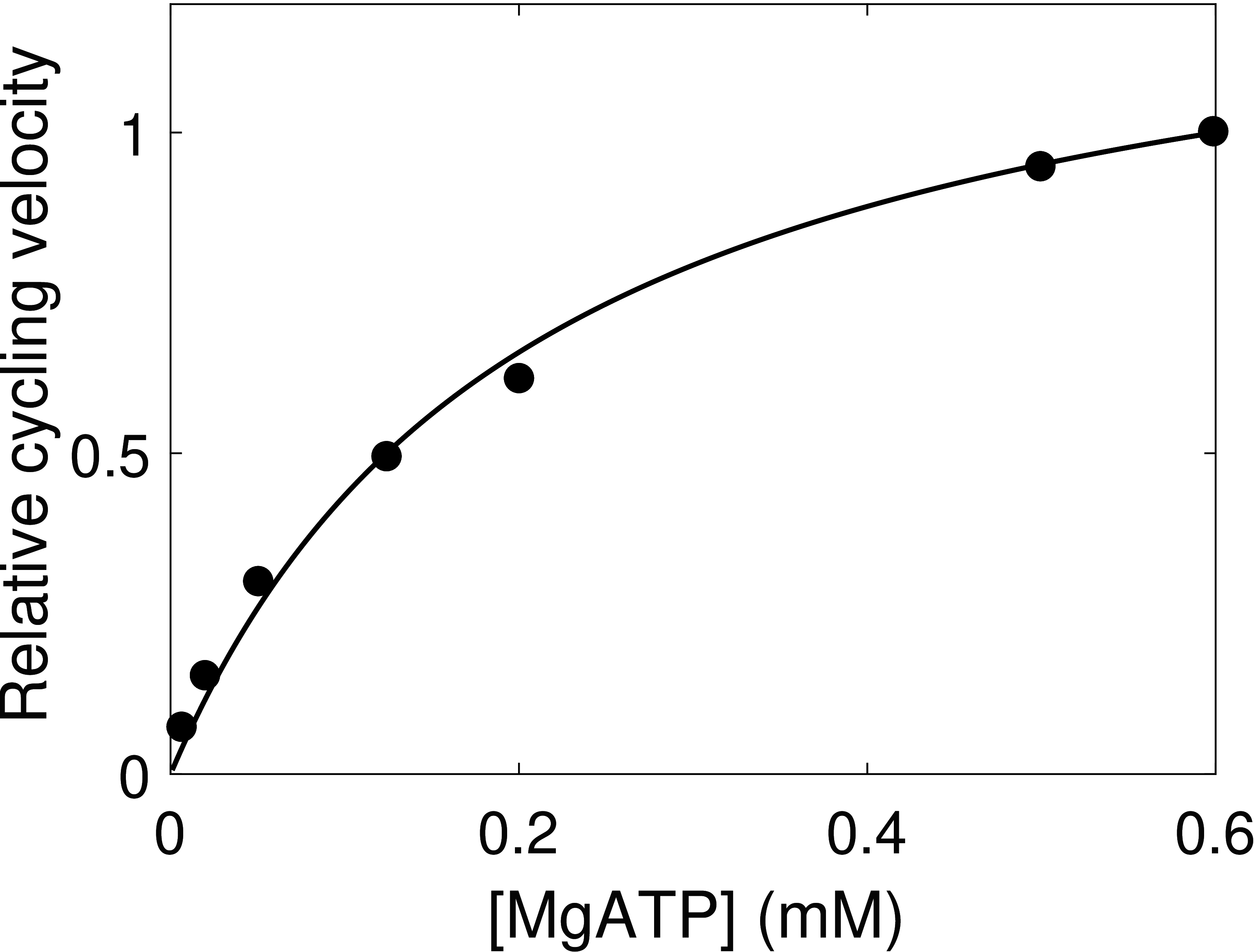 |
Figure 3:Model fit of the updated cardiac Na/K ATPase model to metabolite dependence data. Simulation conditions are displayed on the right of each figure. (A) Comparison of the model to data with varying intracellular sodium concentrations Hansen et al., 2002, Fig. 7(a), normalised to the cycling velocity at . (B) Comparison of the model to data with varying extracellular potassium Nakao & Gadsby, 1989, Fig. 11(a), normalised to the cycling velocity at . (C) Comparison of the model to data with varying ATP Friedrich et al., 1996, Fig. 3(b), normalised to the cycling velocity at .
The response of the updated model to an action potential input was simulated by using an action potential waveform generated from the Luo and Rudy (2000) model Faber & Rudy, 2000Luo & Rudy, 1994 (Figure 4(A)). The original and updated models behave almost identically at resting membrane potentials, but the updated model has a much higher current during the action potential (Figure 4(B)). As noted in Terkildsen (2006), the current of the pump is far lower at physiological intracellular sodium concentrations, thus the pump density needs to be appropriately scaled to be compatible with the Luo-Rudy model. Scaled versions of the Na/K ATPase current within the updated and original models are qualitatively similar to that described using the Luo-Rudy equations Faber & Rudy, 2000Luo & Rudy, 1994, however there are some differences in the resulting waveforms (Figure 4(C)). In particular, the updated model behaves more similarly to the Luo-Rudy Na/K ATPase formulation because it has a more variable current, and thus we hypothesise that under physiological concentrations, the updated model is more compatible with the whole-cell model by Luo and Rudy. A CellML version of the updated model is included with this manuscript.
| A | B | C |
|---|---|---|
![A comparison of the updated cardiac Na^+/K^+ ATPase model to existing models. (A) The action potential waveform used for pump simulation ; (B) The Na^+/K^+ ATPase currents of the original and updated models; (C) A comparison of scaled versions of the updated and original models against the Na^+/K^+ ATPase model in . The pump density was increased by a factor of 3.4 in the updated model, and by a factor of 3.9 in the original model. \mathrm{[Na^+]_i} = 10\si{mM}, \mathrm{[Na^+]_e} = 140\si{mM}, \mathrm{[K^+]_i} = 145\si{mM}, \mathrm{[K^+]_e} = 5.4\si{mM}, \mathrm{pH} = 7.095, \mathrm{[Pi]_{tot}} = 0.8\si{mM}, \mathrm{[MgATP]} = 6.95\si{mM}, \mathrm{[MgADP]} = 0.035\si{mM}, T = 310\si{K}.](https://pub.curvenote.com/df91f02c-1660-414b-b636-0f83e7abfb19/public/LRd_AP_waveform-022e70e72147dd4ada36b8eff6c311d5.png) | 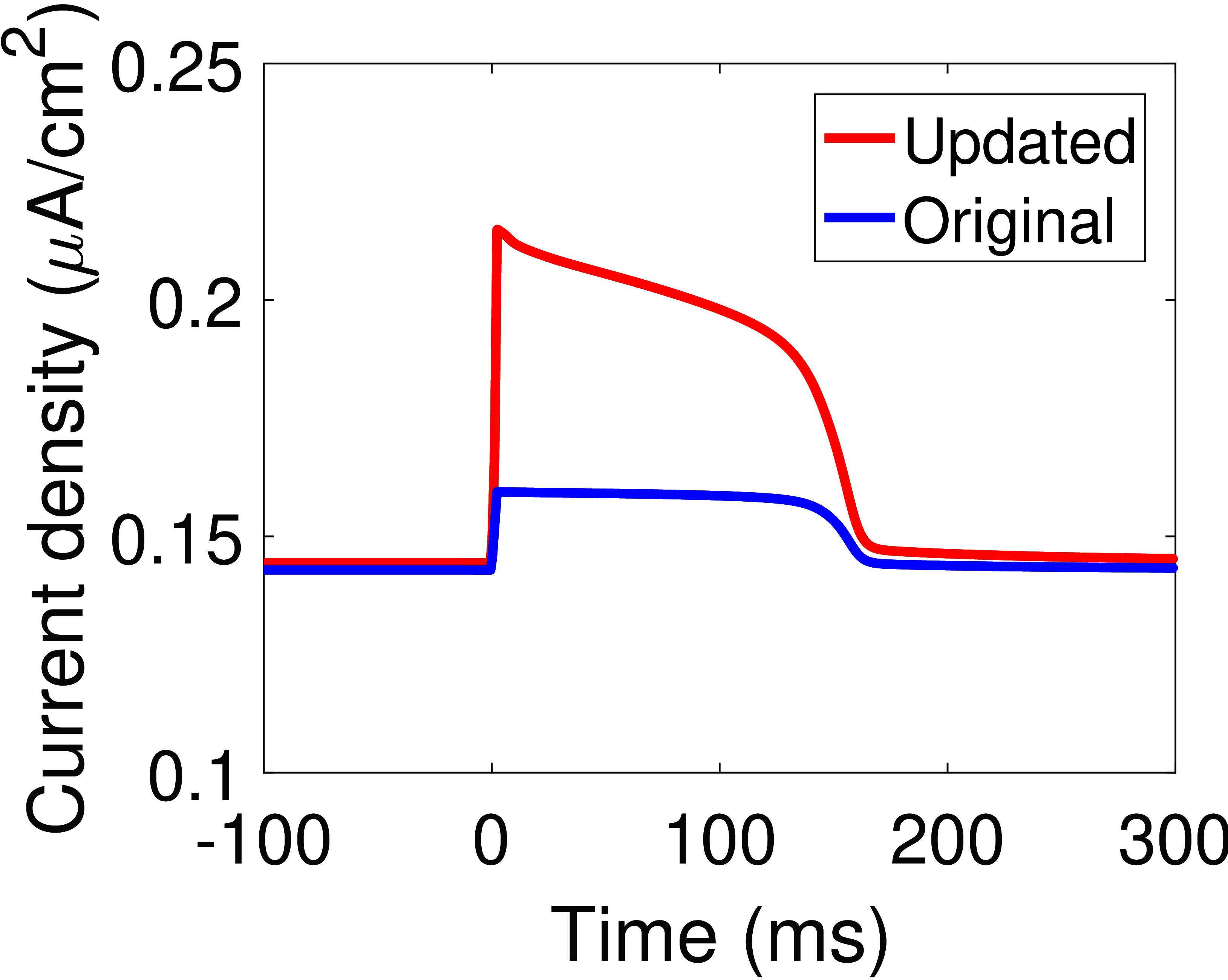 | 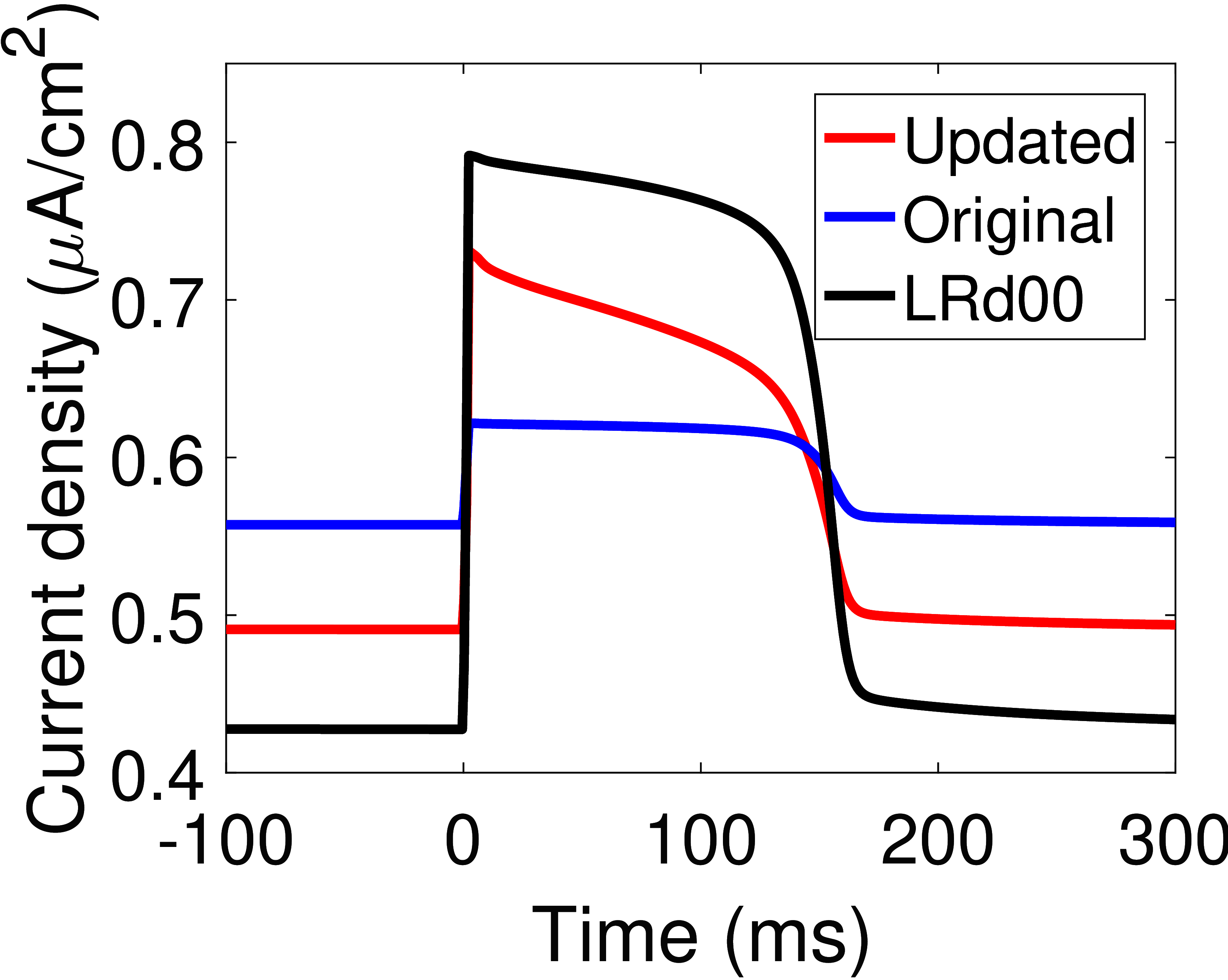 |
Figure 4:A comparison of the updated cardiac Na/K ATPase model to existing models. (A) The action potential waveform used for pump simulation Faber & Rudy, 2000; (B) The Na/K ATPase currents of the original and updated models; (C) A comparison of scaled versions of the updated and original models against the Na/K ATPase model in Faber & Rudy (2000). The pump density was increased by a factor of 3.4 in the updated model, and by a factor of 3.9 in the original model. , , , , , , , , .
![A comparison of the kinetic and bond graph cardiac Na^+/K^+ models. \mathrm{[Na^+]_i} = 50\si{mM}, \mathrm{[Na^+]_e} = 150\si{mM}, \mathrm{[K^+]_i} = 0\si{mM}, \mathrm{[K^+]_e} = 5.4\si{mM}, \mathrm{pH} = 7.4, \mathrm{[Pi]_{tot}} = 0\si{mM}, \mathrm{[MgATP]} = 10\si{mM}, \mathrm{[MgADP]} = 0\si{mM}, T = 310\si{K}. The bond graph model is formulated using concentration ratios thus zero concentrations were approximated by a concentration of 0.001mM to avoid numerical errors.](https://pub.curvenote.com/df91f02c-1660-414b-b636-0f83e7abfb19/public/CellML_comp-2d1ae1e439cb73193957d27a01942074.png)
Figure 5:A comparison of the kinetic and bond graph cardiac Na/K models. , , , , , , , , . The bond graph model is formulated using concentration ratios thus zero concentrations were approximated by a concentration of 0.001mM to avoid numerical errors.
4Bond graph model¶
To verify the physical plausibility of the updated model and to aid incorporation into larger models of cardiac energetics, we have also developed a bond graph version. Bond graphs are an energy-based approach to modelling physical systems, thus they ensure thermodynamic consistency Gawthrop & Crampin, 2014. The structure of the bond graph model is given in Figure 6 of Section 9. The process of converting the model into a bond graph required two notable changes to its representation. Firstly, the bond graph model represents the full unsimplified biochemical cycle, and reactions originally assumed to be in rapid equilibrium were replaced by reactions with fast kinetic parameters that conferred the same equilibrium constant. Thus the bond graph model contains 15 states, and is a close but not exact approximation of the kinetic model. Secondly, because kinetic parameters are often thermodynamically inconsistent Liebermeister et al., 2010, the bond graph approach requires chemical reaction networks to be specified using a different set of parameters: the reaction rate constant and species thermodynamic constant Gawthrop & Crampin, 2014. These parameters always describe thermodynamically consistent systems, regardless of their numerical value. As a result, we converted the kinetic parameters of our model into an equivalent set of bond graph parameters Gawthrop et al., 2015 by using the following matrix equation:
where is the element-wise logarithm operator. The vector contains the kinetic parameters, contains the bond graph parameters, and contains stoichiometric information. The partitions of these matrices are defined as:
where
The matrices and were used to enforce further constraints between the thermodynamic constants of different species, in particular the equilibria of individual ions present within different compartments, and the equilibrium constant of ATP hydrolysis. Assuming that equation (9) can be solved, one possible solution is given by
where is the element-wise exponential operator and is the Moore-Penrose pseudo-inverse of . Since the bond graph framework is energy-based, species must be expressed as molar amounts rather than concentrations to adequately compare energies in different compartments. Therefore we use the diagonal matrix to scale the species thermodynamic constants according to the volume of the compartments they reside in. For consistency with Terkildsen et al. (2007), an intracellular volume of was used for the species , , , , and , an extracellular volume of was used for , , and a constant of 1 was used for each of the pump states.
The bond graph model was simulated under the conditions described in Figure 2(A) to reproduce the curve for , using a slowly increasing membrane voltage to induce quasi-steady-state behaviour. There is a high degree of correspondence between the kinetic and bond graph models (Figure 5). The closeness of the two models suggests that the fast kinetic constants are good approximations of reactions in rapid equilibrium, although we note that the deviation between the bond graph and kinetic models increases slightly at higher cycling velocities when the faster reactions begin to limit flux through the cycle. CellML code describing the bond graph model and reproducing the curve in Figure 5 is provided with this manuscript.
5Conclusion¶
In this manuscript we describe an updated model for the cardiac Na/K ATPase model originally developed by Terkildsen et al. (2007). We have corrected errors with the original model formulation and refitted necessary parameters to ensure that the resulting model is thermodynamically consistent while still recapitulating a wide range of experimental data. We note that the updated model has a natural bond graph representation, and include CellML and MATLAB code for both the kinetic and bond graph models to aid reproducibility. We believe that the thermodynamic consistency and improved reusability of our updated model make it ideal for incorporation into future whole-cell models to study cardiac cell energetics.
6Instructions for running code¶
6.1MATLAB¶
The MATLAB code is located in the MATLAB/code directory. Figures 2–3 can be generated by running the script fit_NaK_parameters.m. Figure 4 can be generated by running NaK_sim.m, and Figure 5 can be generated by running CellML_model_comparison.m.
6.2CellML¶
The figures within this paper can be generated by opening the SED-ML files in OpenCOR. The corresponding figures are referenced within the file names.
8Parameters¶
Table 1:Kinetic parameters for the updated cardiac Na/K ATPase model. Refer to Figure 1 for a schematic.
| Parameter | Description | Value |
|---|---|---|
| Forward rate constant of reaction R6 | ||
| Reverse rate constant of reaction R6 | ||
| Forward rate constant of reaction R7 | ||
| Reverse rate constant of reaction R7 | ||
| Forward rate constant of reaction R13 | ||
| Reverse rate constant of reaction R13 | ||
| Forward rate constant of reaction R15 | ||
| Reverse rate constant of reaction R15 | ||
| Voltage-dependent dissociation constant of intracellular | ||
| Voltage-dependent dissociation constant of extracellular | ||
| Voltage-independent dissociation constant of intracellular | ||
| Voltage-independent dissociation constant of extracellular | ||
| Dissociation constant of intracellular | ||
| Dissociation constant of extracellular | ||
| Dissociation constant of MgATP | ||
| Charge translocated by reaction R5 | ||
| Pump density | Number of pumps per | |
Table 2:Parameters for the bond graph version of the updated cardiac Na/K ATPase model. Parameters were derived by using an intracellular volume of 38pL and an extracellular volume of 5.182pL. Refer to Figure 6 for the bond graph schematic.
| Component | Description | Parameter | Value |
|---|---|---|---|
| R1 | Reaction R1 | ||
| R2 | Reaction R2 | ||
| R3 | Reaction R3 | ||
| R4 | Reaction R4 | ||
| R5 | Reaction R5 | ||
| R6 | Reaction R6 | ||
| R7 | Reaction R7 | ||
| R8 | Reaction R8 | ||
| R9 | Reaction R9 | ||
| R10 | Reaction R10 | ||
| R11 | Reaction R11 | ||
| R12 | Reaction R12 | ||
| R13 | Reaction R13 | ||
| R14 | Reaction R14 | ||
| R15 | Reaction R15 | ||
| Pump state ATP–Ei K2 | |||
| Pump state ATP–Ei K1 | |||
| Pump state ATP–Ei | |||
| Pump state ATP–Ei Na1 | |||
| Pump state ATP–Ei Na2 | |||
| Pump state ATP–Ei Na3 | |||
| Pump state P–Ei (Na3) | |||
| Pump state P–Ee Na3 | |||
| Pump state P–Ee Na2 | |||
| Pump state P–Ee Na1 | |||
| Pump state P–Ee | |||
| Pump state P–Ee K1 | |||
| Pump state P–Ee K2 | |||
| Pump state Ee (K2) | |||
| Pump state ATP–Ee (K2) | |||
| Ki | Intracellular | ||
| Ke | Extracellular | ||
| Nai | Intracellular | ||
| Nae | Extracellular | ||
| Intracellular MgATP | |||
| Intracellular MgADP | |||
| Free inorganic phosphate | |||
| H | Intracellular | ||
| mem | Membrane capacitance | ||
| zF_5 | Charge translocated by R5 | ||
| zF_8 | Charge translocated by R8 | ||
9Bond graph model structure¶

Figure 6:Bond graph structure of the cardiac Na/K ATPase model. Pump states are coloured in blue, and reactions are coloured in green. The names for these components are consistent with their labels in Figure 1.
Acknowledgments¶
This research was supported in part by the Australian Government through the Australian Research Council’s Discovery Projects funding scheme (project DP170101358), an Australian Government Research Training Program Scholarship to M.P., and a Research Fellowship (1692) from the Heart Foundation of New Zealand to K.T.
- Terkildsen, J. R., Crampin, E. J., & Smith, N. P. (2007). The balance between inactivation and activation of the Na+-K+ pump underlies the triphasic accumulation of extracellular K+ during myocardial ischemia. American Journal of Physiology - Heart and Circulatory Physiology, 293(5), H3036–H3045. 10.1152/ajpheart.00771.2007
- Terkildsen, J. (2006). Modelling Extracellular Potassium Accumulation in Cardiac Ischaemia [Masters Thesis]. The University of Auckland.
- Smith, N. P., & Crampin, E. J. (2004). Development of models of active ion transport for whole-cell modelling: cardiac sodium–potassium pump as a case study. Progress in Biophysics and Molecular Biology, 85(2–3), 387–405. 10.1016/j.pbiomolbio.2004.01.010
- Nakao, M., & Gadsby, D. C. (1989). [Na] and [K] dependence of the Na/K pump current-voltage relationship in guinea pig ventricular myocytes. The Journal of General Physiology, 94(3), 539–565. 10.1085/jgp.94.3.539
- Hansen, P. S., Buhagiar, K. A., Kong, B. Y., Clarke, R. J., Gray, D. F., & Rasmussen, H. H. (2002). Dependence of Na+-K+ pump current-voltage relationship on intracellular Na+, K+, and Cs+ in rabbit cardiac myocytes. American Journal of Physiology - Cell Physiology, 283(5), C1511–C1521. 10.1152/ajpcell.01343.2000
- Friedrich, T., Bamberg, E., & Nagel, G. (1996). Na+,K+-ATPase pump currents in giant excised patches activated by an ATP concentration jump. Biophysical Journal, 71(5), 2486–2500. 10.1016/S0006-3495(96)79442-0
- Lloyd, C. M., Halstead, M. D. B., & Nielsen, P. F. (2004). CellML: its future, present and past. Progress in Biophysics and Molecular Biology, 85(2–3), 433–450. 10.1016/j.pbiomolbio.2004.01.004
- Oster, G., Perelson, A., & Katchalsky, A. (1971). Network thermodynamics. Nature, 234(5329), 393–399.
- Gawthrop, P. J., & Crampin, E. J. (2014). Energy-based analysis of biochemical cycles using bond graphs. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 470(2171), 20140459. 10.1098/rspa.2014.0459
- Gawthrop, P., & Smith, L. (1996). Metamodelling: for bond graphs and dynamic systems. Prentice Hall.
- Borutzky, W. (2010). Bond Graph Methodology. Springer.
- Gawthrop, P. J., & Bevan, G. P. (2007). Bond-graph modeling. IEEE Control Systems, 27(2), 24–45. 10.1109/MCS.2007.338279
- Apell, H. J. (1989). Electrogenic properties of the Na,K pump. The Journal of Membrane Biology, 110(2), 103–114. 10.1007/BF01869466
- Keener, J., & Sneyd, J. (2009). Mathematical Physiology (S. S. Antman, J. E. Marsden, & L. Sirovich, Eds.; Vol. 8/1). Springer New York.
- Tran, K., Smith, N. P., Loiselle, D. S., & Crampin, E. J. (2009). A Thermodynamic Model of the Cardiac Sarcoplasmic/Endoplasmic Ca2+ (SERCA) Pump. Biophysical Journal, 96(5), 2029–2042. 10.1016/j.bpj.2008.11.045





